ANALISIS REGRESI SEDERHANA
1. Pengertian
Analisis regresi linier sederhana adalah hubungan secara linear antara satu variabel independen (X) dengan variabel dependen (Y). Analisis ini untuk mengetahui arah hubungan antara variabel independen dengan variabel dependen apakah positif atau negatif dan untuk memprediksi nilai dari variabel dependen apabila nilai variabel independen mengalami kenaikan atau penurunan.. Data yang digunakan biasanya berskala interval atau rasio.
Rumus regresi linear sederhana sebagi berikut:
Y’ = a + bX
Keterangan:
Y’ = Variabel dependen (nilai yang diprediksikan)
X = Variabel independen
a = Konstanta (nilai Y’ apabila X = 0)
b = Koefisien regresi (nilai peningkatan ataupun penurunan)
Contoh kasus:
Seorang mahasiswa bernama Hermawan ingin meneliti tentang pengaruh biaya promosi terhadap volume penjualan pada perusahaan jual beli motor. Dengan ini di dapat variabel dependen (Y) adalah volume penjualan dan variabel independen (X) adalah biaya promosi. Dengan ini Hermawan menganalisis dengan bantuan program SPSS dengan alat analisis regresi linear sederhana. Data-data yang di dapat ditabulasikan sebagai berikut:
Tabel. Tabulasi Data Penelitian (Data Fiktif)
No
|
Biaya Promosi
|
Volume Penjualan
|
1
|
12,000
|
56,000
|
2
|
13,500
|
62,430
|
3
|
12,750
|
60,850
|
4
|
12,600
|
61,300
|
5
|
14,850
|
65,825
|
6
|
15,200
|
66,354
|
7
|
15,750
|
65,260
|
8
|
16,800
|
68,798
|
9
|
18,450
|
70,470
|
10
|
17,900
|
65,200
|
11
|
18,250
|
68,000
|
12
|
16,480
|
64,200
|
13
|
17,500
|
65,300
|
14
|
19,560
|
69,562
|
15
|
19,000
|
68,750
|
16
|
20,450
|
70,256
|
17
|
22,650
|
72,351
|
18
|
21,400
|
70,287
|
19
|
22,900
|
73,564
|
20
|
23,500
|
75,642
|
Langkah-langkah pada program SPSS
Ø Masuk program SPSS
Ø Klik variable view pada SPSS data editor
Ø Pada kolom Name ketik y, kolom Name pada baris kedua ketik x.
Ø Pada kolom Label, untuk kolom pada baris pertama ketik Volume Penjualan, untuk kolom pada baris kedua ketik Biaya Promosi.
Ø Untuk kolom-kolom lainnya boleh dihiraukan (isian default)
Ø Buka data view pada SPSS data editor, maka didapat kolom variabel y dan x.
Ø Ketikkan data sesuai dengan variabelnya
Ø Klik Analyze - Regression - Linear
Ø Klik variabel Volume Penjualan dan masukkan ke kotak Dependent, kemudian klik variabel Biaya Promosi dan masukkan ke kotak Independent.
Ø Klik Statistics, klik Casewise diagnostics, klik All cases. Klik Continue
Ø Klik OK, maka hasil output yang didapat pada kolom Coefficients dan Casewise Diagnostics adalah sebagai berikut:
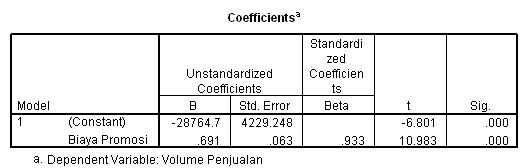
Tabel. Hasil Analisis Regresi Linear Sederhana
Persamaan regresinya sebagai berikut:
Y’ = a + bX
Y’ = -28764,7 + 0,691X
Angka-angka ini dapat diartikan sebagai berikut:
- Konstanta sebesar -28764,7; artinya jika biaya promosi (X) nilainya adalah 0, maka volume penjulan (Y’) nilainya negatif yaitu sebesar -28764,7.
- Koefisien regresi variabel harga (X) sebesar 0,691; artinya jika harga mengalami kenaikan Rp.1, maka volume penjualan (Y’) akan mengalami peningkatan sebesar Rp.0,691. Koefisien bernilai positif artinya terjadi hubungan positif antara harga dengan volume penjualan, semakin naik harga maka semakin meningkatkan volume penjualan.
Nilai volume penjualan yang diprediksi (Y’) dapat dilihat pada tabel Casewise Diagnostics (kolom Predicted Value). Sedangkan Residual (unstandardized residual) adalah selisih antara Volume Penjualan dengan Predicted Value, dan Std. Residual (standardized residual) adalah nilai residual yang telah terstandarisasi (nilai semakin mendekati 0 maka model regresi semakin baik dalam melakukan prediksi, sebaliknya semakin menjauhi 0 atau lebih dari 1 atau -1 maka semakin tidak baik model regresi dalam melakukan prediksi).
- Uji Koefisien Regresi Sederhana (Uji t)
Uji ini digunakan untuk mengetahui apakah variabel independen (X) berpengaruh secara signifikan terhadap variabel dependen (Y). Signifikan berarti pengaruh yang terjadi dapat berlaku untuk populasi (dapat digeneralisasikan).
Dari hasil analisis regresi di atas dapat diketahui nilai t hitung seperti pada tabel 2. Langkah-langkah pengujian sebagai berikut:
1. Menentukan Hipotesis
Ho : Ada pengaruh secara signifikan antara biaya promosi dengan volume penjualan
Ha : Tidak ada pengaruh secara signifikan antara biaya promosi dengan volume penjualan
2. Menentukan tingkat signifikansi
Tingkat signifikansi menggunakan a = 5% (signifikansi 5% atau 0,05 adalah ukuran standar yang sering digunakan dalam penelitian)
3. Menentukan t hitung
Berdasarkan tabel diperoleh t hitung sebesar 10,983
4. Menentukan t tabel
Tabel distribusi t dicari pada a = 5% : 2 = 2,5% (uji 2 sisi) dengan derajat kebebasan (df) n-k-1 atau 20-2-1 = 17 (n adalah jumlah kasus dan k adalah jumlah variabel independen). Dengan pengujian 2 sisi (signifikansi = 0,025) hasil diperoleh untuk t tabel sebesar 2,110 (Lihat pada lampiran) atau dapat dicari di Ms Excel dengan cara pada cell kosong ketik =tinv(0.05,17) lalu enter.
5. Kriteria Pengujian
Ho diterima jika –t tabel < t hitung < t tabel
Ho ditolak jika -thitung < -t tabel atau t hitung > t tabel
6. Membandingkan t hitung dengan t tabel
Nilai t hitung > t tabel (10,983 > 2,110) maka Ho ditolak.
7. Kesimpulan
Oleh karena nilai t hitung > t tabel (10,983 > 2,110) maka Ho ditolak, artinya bahwa ada pengaruh secara signifikan antara biaya promosi dengan volume penjualan. Jadi dalam kasus ini dapat disimpulkan bahwa biaya promosi berpengaruh terhadap volume penjualan pada perusahaan jual beli motor.